Phase Locking Value (PLV) is a statistic that can be used to investigate task-induced changes in long range synchronization of neural activity from EEG data. This method is introduced in Lachaux et al., (1999). I have implemented the computation of this statistic in MATLAB and you can download it from the link below. In this post, I will talk a little bit about how PLV can be useful when analyzing EEG data. Note that this statistic may also be used to quantify LFP (local field potential) data recordings to study synchrony at a finer scale compared to EEG.

It is useful to keep in mind a few properties of the PLV statistic before diving in further.
- PLV statistic is a time course. This means that for every time point in your EEG data, you can extract a measure of connectivity. Therefore, this quantity can be used to observe transient changes in connectivity without pre-defining a time window of analysis.
- One PLV time course for every electrode pair. For example, if data is recorded from 28 EEG electrodes, there are 378 possible PLV time courses.
- One PLV time course is computed over multiple trials. In practice, I have observed that this metric is suitable for datasets with a large number of trials. It is good to have a few hundred trials for each experimental condition for which long range synchronization is to be quantified using PLV.
The PLV statistic can be argued to be a proxy for connectivity. Intuitively, if the EEG signal in two channels (electrodes) during an experimental condition rises and falls together more than a baseline value, then there is more synchronization or loosely speaking, enhanced connectivity between these two electrodes. If it is less than the baseline value, there is desynchronization or loosely speaking, decreased connectivity between the two electrodes. Note that this metric does not care about the co-variation in the power of the EEG signal between two electrodes.
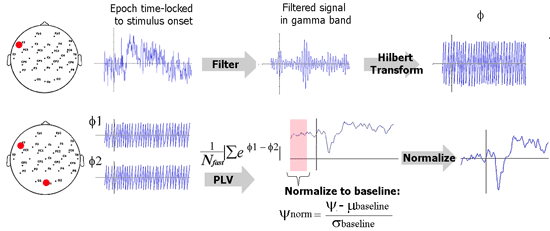
The schematic below illustrates how PLV is computed in this implementation. Explanation for each step follows.
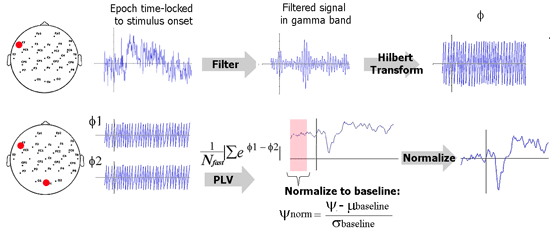
Filtering. The EEG data is first filtered in the desired frequency band of interest, for example, gamma band, 35-45 Hz. In practice, it is best to use an FIR (finite impulse response) filter to filter such data in comparison to IIR (infinite impulse response) filters. Loosely speaking, FIR filters filter the signal in time domain and IIR filters operate in the frequency domain. Put simply, an FIR filters computes the value of the filtered signal at a time point from the values of the previous and future points. How far the FIR filter looks is knows as the order of the FIR filter. For EEG signals, a useful rule of thumb is to ‘look at’ about 4 to 5 cycles of the desired EEG rhythm. As an example, consider gamma rhythm (35-45 Hz). Here, one cycle is about 25 ms and I would set the order of the filter to be 100 ms. If the sampling rate is 500 Hz, then the filter order would be 50 data points.
Hilbert transform. This step is used to quantify rising and falling of EEG data. Hilbert transform of a signal can be used to compute the instantaneous amplitude as well as the instantaneous phase. We ignore the former and use the phase (φ) for PLV computation. φ is a value between –π and π. Think of the filtered EEG signal as a series of crests and troughs. A value of π indicates the peak of a crest and a –π indicates the bottom of a trough.
PLV metric. Remember that there is a phase time course φ for every EEG electrode. Now consider the phase time courses of two electrodes. The difference between these two time courses (Δφ) quantifies locking between the phases of these two electrodes. If an experimental stimulus influences signal in two electrodes to rise and fall together or with a certain lag, then Δφ will be consistent between trials. If there is absolutely no relationship between when the signal in these two electrodes will rise and fall, then Δφ will be random. All we need to do now is to quantify the randomness in Δφ. This can be done using a little trick from complex number theory. Please see the equation in the analysis schematic to understand this trick.
Normalization. This step is performed to make the PLV metric useful in practice. Note that due to its definition, PLV is always a value between 0 and 1; 0 signifying purely random rise and fall whereas a value of 1 signifies that one signal perfectly follows the other. In practice, the value of a PLV obtained is going to vary very little over time and the absolute PLV is not what we are interested in. We are interested in knowing whether an experimental stimulus induced a change in PLV. We are interesting in answering questions such as “was there increased connectivity between the frontal and parietal electrodes when the subject performed a task?” . To find this, we should test if PLV after stimulus is significantly greater than the PLV before stimulus. To simplify things, we can use the pre-stimulus period as a baseline and perform a z-transform normalization.
Good luck!
Dear Praneeth Namburi,
I am studing the Phase Locking Value you posted on your blog, and regarding it’s dynamical feature is really amazing…
I have just a simple question. Despite it’s dynamical feature, if I want to have only one value for each pair of electrodes can I take the mean value of the Phase Locking “Signal”.
I ask you because I haven’t studied the PLV deeply, so you can probably detect if there is an error on my thought.
I am waiting for your answer as soon as possible.
Best Regards
Manousos
Dear Manousos,
Thank you for your interest in the PLV.
Regarding having only one value for a pair of electrodes, you can of course average the PLV time course between two time points, say from 100 ms to 120 ms to get an ‘average’ phase locking value. But, you may reduce the sensitivity of the PLV.
And regarding getting PLV 1 for any pair of electrodes, here is a couple of things you should check:
1) Did you filter your signal in the correct frequency range? (remember, don’t make the range ‘too’ narrow)
2) How many trials did you have? I had about 500 to 600 trials. In practice it is best if you have a large number of trials. This can be thought of as a disadvantage to using PLV, in the sense that you get one time course over many trials, and I don’t know of any way to get single trial connectivity.
If you have only one trial, mathematically, the PLV would be 1. In simple terms, PLV is measuring the ‘consistency’ in the phase difference between two electrodes, and consistency is measured across trials. If there is only one trial, then of course the phase difference is consistent over one trial and you would get a PLV value of 1.
Please don’t hesitate to contact me if you have any other questions. Good luck with your PLV computations!
Yours Sincerely,
Praneeth
Hi Praneeth
I have just one trial, rather one continuous data segment. So, in order to determine the PLV, can I break the data into segments using moving window technique and then compute the PLV ?
Hi Narayan,
Thanks for your comment.
For the technique I’ve outlined here, you must have many trials, ideally a few hundred. The idea is to find how connectivity changes relative to a certain event in your experiment, such as stimulus presentation, or response given by your subject. Technically, the moving window technique will give you results, but I am not sure if it would give you anything meaningful. Are you trying to quantify connectivity between brain regions during sleep or another such continuous recording? In this case, perhaps coherence measures may be more helpful or in special cases depending on the question you are trying to answer, you can use the suggestion below.
PLV is useful mostly for data collected across multiple repeats of a particular manipulation. This can be anything, even a particular signature in the EEG signal, such as the phase of a slower oscillation. For example, you could extract epochs of gamma-band filtered data locked to the phase of theta oscillation or amplitude of delta oscillations; then compute PLV time course relative to these. If you just use a constant sized moving window, you should in theory see a flat PLV time course.
Hope this helps. Good luck and let me know if you have any other questions.
Yours Sincerely,
Praneeth
Hey Praneeth
Thanks for the prompt reply. I am actually analyzing epilepsy data ( the ictal period , mainly). I have decomposed the signal into independent components using ICA. Now I am trying to determine those independent components with highest phase synchrony. So, in a way, I guess moving window might make sense then ?
As you mention about particular ‘signature’, here the signature is the ictal period, which are long , repeated oscillations.
Hi Narayan,
Sure, ictal onsets can be used as ‘events’. If you isolate all ictal onsets from your EEG signal (or independent components) and compute PLV, you might find a significant change in connectivity within a particular network upon ictal onset.
Are you trying to show that connectivity between certain regions is different during the ictal period, relative to inter-ictal periods? If so, then your moving window idea may be viable.
One useful point to remember about PLV: It is used for measuring synchrony (especially changes in synchrony) across brain regions/electrodes. It will not give you any insight into synchrony where all nearby neurons synchronize their neuronal discharges and manifest as large-amplitude oscillations in your electrodes.
I brought up this point because I am not very clear on using PLV with your independent components. If you are trying to localize different foci for the seizure onset and look at how interactions between them is different between ictal and inter-ictal periods, then I understand the motivation behind using PLV on your ICA components.
Good luck and let me know if you have any other questions.
Yours Sincerely,
Praneeth
Hi,
Regarding PLV method and your code, i sent a meessage to praneeth-at-mit-dot-edu. i wonder if this is correct email adders?
Hi Mario, Thank you for your query. I just replied to your email.
Hello
I try use the script of PLV, but I get this error :
??? Error using ==> mtimes
Inner matrix dimensions must agree.
Error in ==> firls at 80
cos_ints = [omega; sin((1:N)’ * omega)];
Error in ==> fir1 at 98
hh = firls(L-1,ff,aa);
I have a eeg signal in 512 Hz
Can you help me?
Best Regards
Pablo Burgos
Dear Pablo,
Thank you for your question. I need more information about your data before I can figure out why is script is not working. Here are some things to check:
1) Are the dimensions of the input data correct (i.e., are time points of the signal in the second dimension?)
2) Check the order of your FIR filter and the number of samples. Please make sure the number of time samples in the signal (second dimension of the matrix) is a few times the FIR filter order.
Kindly let me know if this helps. If it doesn’t work, it would be great if you can send me your eeg matrix in a file. That would make it easier for me to diagnose the problem.
Good luck and let me know if you have more questions!
Praneeth
Dear Praneth,
I fix the problem, change the order of seth path of matlab. If external toolbox like eeglab or fieldtrip are in the top of the seth path the function fir1 don´t work. I share this information for prevent to other users.
kind regards
Dear Pablo:
Thank you very much. I have the same problem and I have no idea the reason. This helps me a lot.
Same issue with the Matlab path… Thank you for clarifying, Pablo! Great tool, Praneeth!
Best,
Marcus
Hi Praneeth,
Many thanks for this useful toolbox. However, I have one question regarding the computation of PLV. According to this article (http://www.jneurosci.org/content/27/11/2858.long), they computed the phase difference by multiplying the phase the the first sensor with the complex conjugate of the second sensor. I wondered what is the difference from Lachaux’s method. I tried to compute the phase difference in both Lachaux’s and Melloni’s equations but got different results. Could you shed some light on this? many thanks!
Shen-Mou
Hi Shen-Mou,
Thanks for your question. Mathematically, there shouldn’t be a difference, unless I missed something. I took a quick look at the article, and they cite Lachaux’s paper which uses this method and they don’t mention that they did anything different. Was your phase (angle) computation method the same in both cases? I was using Hilbert transform and calculating the angle from that signal.
Hope this helps.
Praneeth
Hi Praneeth,
I’m currently researching the coherence between EMG and EEG during muscle fatiugue. I’m trying to prove that using PLV would be a better measure then coherence. Since this involves muscle fatigue I can only have one trial till the subject fatigues.
The question I have is,
1.is it correct to use PLV for emg-eeg?
2.and also is it ok to use a moving window for such a case?
Also thanks so much for your blog, it really helps.
Thanks
Hi Jeff, Thank you for your comment.
1) I have not measured coherence between EEG and EMG before. Technically, you can compute it, but I’m not sure how I would interpret the result. When you are computing phase locking between two regions of the brain (say frontal regions and occipital regions in the gamma band) – this “could” correspond to long range synchronization between these two regions. Moreover, theoretically possible mechanisms for this synchronization can be attributed to distinct neuronal populations in the brain. I don’t know much about muscles, but if you can interpret your data long similar lines, then it may be valid to compute a coherence value between EEG and EMG (but not PLV, at lease on the type of data you’re describing – see below).
2) The way PLV is defined, you need many trials and is suited to analyze data from repeated presentations of a stimulus. If you take a moving window to define “pseudo-trials”, your PLV time course will highly depend on the size of the moving window and this is why (as far as I can see) it is not suitable to use PLV on the type of data that you’re describing.
I’m really glad to hear that my blog helped you. Hope this helps a bit more. Good luck with your work!
Cheers,
Praneeth
Hi Praneeth,
I’m searching for book sources which include PLV. I can only find papers but I like books more ;). Do you know one which you can recommend?
Thanks a lot.
Janine
Hi Janine,
Unfortunately I’m only aware of papers that use PLV. I worked with PLV a lot 4 years ago and at that time, I wasn’t aware of any books that had a good description of PLV. As mentioned in the blog post, I highly recommend the Lachaux 1999 paper for learning about PLV.
Let me know if I can help with anything else. Good luck.
Praneeth
Hi Praneeth,
I often use wavelet to get phase information. I found that using hilbert can get phase information of precision equal to sampling rate. Could I treat the phase of each time point as the reflection of phase at that time?
Another question is that to get phase in theta band, I use a bandpass filter with very narrow pass band. would this filtering process distort phase locking value I get?
Hi Xiangbin,
Yes, when using hilbert transform, I usually treat the phase I get at each time point as the phase of that time point – but remember that the hilbert transform algorithm probably peeked at the signal a little before and after that time point.
The answer to your next question is that it ‘depends’ on the exact filter that you use. Usually, in my experience, I have not found any issues with using narrow pass bands as small as 4 to 5 Hz. Only recommendation from my side (if you’re dealing with non-stationary signals such as EEG signals) is that you use FIR filters instead of IIR filters. Also, at such low frequencies (relative to say gamma band), it is essential that you do zero-phase filtering. You can simply do this in 3 steps (1) apply the FIR filter to your signal (2) invert your signal in time and (3) re-apply the FIR filter and invert your signal back. This will double the order of the FIR filter that you are using but it will not introduce any phase shifts.
Hope this helps.
Praneeth
Hi
Another possibility is to use wavelet decomposition to extract EEG sub-bands, which is also filtering operation internally.And then I compute the PLV.
Hello Sir,
I have 14 channel EEG data during single player gaming and I want to apply PLV but I have confusion in number of trials and number of time points . Please clarify that how can I use this in my research? The sampling rate of my data is 128 samples/sec.
If there is an event repeating in the game (for example, when the player jumps), I would segment out an interval around that event and call that one trial. If the player jumps 317 times in the game total, then I have 317 trials. And if I segment EEG signal -1 second to 1 second where 0 is when the player jumped, then each trial would have 256 samples. Hope this helps.
Praneeth
Hello Sir,
I am a student of B.tech ECE and currently doing my training as part of curriculum and my project is on EEG.I have been told to study PLV which is slightly difficult for me to understand at this point of time as i have no previous knowledge of this topic.Can you please help with this and tell me from where i should start studying so as to understand this topic better.I’ll be grateful to you
Regards,
Neha kasana
Hi Neha,
Did the paper Lachaux et al., (1999) and my blog entry not help? I used this technique more than 5 years back and I haven’t kept up with the latest papers / textbooks in this field. Here are a couple of leads that can be useful for you:
“EEG Analysis – Theory and practice” Chaptre 58 of Electroencephalography 5th ed – E. Niedermeyer, F. da Silva (Lippincott, 2005)
I found this dissertation (of Gleb V. Tcheslavski) just now that could help you: http://scholar.lib.vt.edu/theses/available/etd-12202005-192214/unrestricted/Dissertation.pdf
Hope this helps.
Praneeth
Thanks sir,i’ll definitely go through the link u have suggested
Hi Praneeth,
Thank you for having posted this. I was wondering whether this script can be applied to cross-frequency phase-phase coupling (see http://www.ncbi.nlm.nih.gov/pubmed/22238079) instead of within-frequency phase synchronization for which the script was written. Please let me know your thoughts.
Alex
Hi Alex, In principle, yes. However, you may need to make a couple of modifications to either your data or my script. Here is how I would change the data. Let’s say you have 32 channel data. You can duplicate this data prior to filtering (now your data has 64 channels). You can then filter the first 32 channels in one frequency range (say theta) and the next 32 channels in another frequency range (say gamma). Now, you can apply my script, and the PLV between channels 1 and 34 will actually be cross frequency phase coupling between channels 1 and 2. Hope this helps.
Dear,
I have 14 channel,3225 time points,2 trials.whenever i try 2 run this program(the function part).I get error index exceeds matrix dimensions and error in line 8 of the function that was used in the example given by you.please help.
Hi, I think this is because your data has only 14 channels, and line 8 in my example is trying to plot the phase locking value between channels 17 and 20. You can change these numbers to 12 and 14, and the example should run just fine. Also, I would not recommend using phase locking value on data that has only 2 trials. Hope this helps.
Hi
Dear Praneeth,
I have a BCI EEG data contain 1min eye open baseline and 4-2min separate continuous tasks.
so regarding to your answer to Manousos i want to know can i use plv for all pair-wise combinations of channels of my data???
best regards
Atiye
Of course, there is no restriction on how many channel pairs you have. You only need to be cautious of the low number of trials in your data. If you have several repetitions, then perhaps using PLV makes sense.
Hey,praneeth
I have ERP data..can i apply plv on it and will it be efficient??
In my view, ERP and PLV are capturing / highlighting different aspects of information within the EEG data. When I analyzed my data set, I used a Fourier transform to determine the frequency range of ERPs – this was usually < 30 Hz. I only used PLV on frequency bands that were "not contaminated" by ERPs (35-45 Hz). The logic I used at the time was that ERPs can be caused by a "phase resetting event", which, in principle, is different from a phase locking event.
I'm not sure if this helped, so here is a short version: If you have ERP data before averaging, then you can filter your data and apply the PLV script. How you interpret the results is slightly more tricky, and depends on the frequency bands in which you are studying phase locking.
Thanks for posting this script. I have analysed ERPs a lot but I have recently wanted to look at connectivity using PLVs. However, I have no experience of dealing with data on matlab (I’ve used NeuroScan and BrainVision) and I would therefore want to find a place where maybe all the steps are explained through to the application of the PLV script. Do you know anywhere where such a tutorial (in full or where I could find bits for each processes)? Or anyone to contact who would be willing to guide me through such an analysis. I know it’s a lot to ask because it’s all very complex but without knowledge of much matlab at all I feel like I can never learn.
Hi Bastien, Hope you had some luck figuring out your data and scripts. MATLAB can be a really useful tool and I am planning to post some tutorials on using MATLAB within the context of neuroscience. Sorry I can’t be of more help. Good luck.
thanks for the information, it is so hepfull!!! 😀
You’re welcome Omar 🙂
Hi!
thanks for posting this. It will greatly ease my work. Just a question (although I think I aready figured out the answer): The normalization step you discribe in the post, is NOT included in the script, is it?
Oh, and is there a specific reason you did not implement PLS (as proposed by Lachaux) as well. I did it, and it was quite low effort, given what you already have. If you want to includ it in your code, mail me.
Greetings
Nils
Hi Nils, You are right, I didn’t implement the normalization step in the script. Thank you, perhaps you can post an implementation of phase locking statistic here, and people can use it?
Hi Praneeth. Thank you for the MATLAB code. I am applying the code for one of my projects, and so I was wondering how can I cite your code? Thanks!
You’re welcome! I didn’t publish this work, so unless you can cite my blog, don’t worry about it. Thank you for asking 🙂
Hi Praneeth,
Thanks for coding such a beautiful concept.
I am working on eeg data obtained when a person is meditating. That means there is no visual stimuli or any other stimuli as mentioned in the paper Lachaux et al., (1999) . And as far as i understand ,the PLV can be calculated when u have a lot of trails of a similar event. But meditation involves only one trail. Can I segment the data into 1 second windows and use each of the segments as trails.
Please help!!.
Regards.
Hi Subodh, please see Lachaux et al. (2000) titled “Studying single trials of phase synchronous activity in the brain”. Thanks to Carolina Kunicki for pointing this out to me.
Hi Praneeth,
your work is amazing and usefull. i ran succesfully your script on my data, but the meanig of the plot is still unclear and my question could result stupid.
the blue and the green lines obtained from the plv do represent the “attended” and the ” ignored” condition?
If you had two conditions in your data set, then yes, you are correct 🙂
Hi Praneeth,
I can’t thank you enough for generously sharing your script and follow up discussions!
I have also a simple question for you: the resulted figure from example.m script shows a high PLV value( ~0.8) at fist and then drops to 0.1. Do you think it is an artifact (e.g, filter !) or it has real meaning for the data?
Hello Praneeth,
I’m not sure if I completely understood about the PLV. I thought that when you run the function, it calculates the PLVs for all the channels and then you plot the specific PLV for 2 channels. So I thought that the plot would be a single signal corresponding to the PLV for channels 17 and 20 (as it is in the example), but in fact there are two signals (very similar, but different) when I run the example you give in the script. Where am I confused?
Thank in advance!!
Borja
Hello Praneeth,
Thanks so much for sharing this script. As someone who is still a Matlab / EEG novice, I have a perhaps silly question. I am confused as to what exactly to run the script on. I have several CNT files that I work with in eeglab – do I save those files as the eegData variable to be used in the script? I guess what I’m asking is whether the CNT data is actually the 3D matrix referred to in your script?
I was also wondering if your script performs a Hilbert / wavelet transform or should be run after that step is completed.
Hopefully that makes sense – thanks so much!!!
Rachel
Hi Rachel, I didn’t make this into an EEGLAB plugin, so it doesn’t actually take in a CNT file. You should load the CNT file and then get the data in the form of a MATLAB matrix. The script actually does FIR filtering and Hilbert transform. You just need to specify the frequency limits of your filters. Hope you got a chance to look at the example given at the beginning of the script. If not, just open the script in any text editor and read through the commented lines at the top. Hope this helps.
Thanks! That helps
Whoops, I also wanted to check if your script performs a Hilbert / wavelet transform or should be run after that step is completed?
Duh, just saw you had that in your answer. Thanks again!
Hello Praneeth Sir
I’m new at this and the question that I’m about to ask may be trivial in nature.
I have a 16 electrode EEG data with me. It is two dimensional. But, I see that I require three dimensional data to run this code, the third dimension being the number of trials, as you’ve mentioned.
I’m a bit confused about this trials concept. How should I know how many trials I need? Should I pick a random number?
Also, if I want to convert my 2-dimensional data matrix into 3-dimensional, I would need to add another dimension or an array (whose size would be equal to the number of trials) to my already existing 2-dimensional data. Now what should be the values of this array?
I would be really thankful if you would help me with this.
Thank You!
Phase locking value is meant to be used for analyzing data from experiments with multiple presentations of the same/similar stimuli. If your experiment has such “trials”, then you can extract snippets of data from your 16 channel recordings, and the number of trials will be your third dimension. Hope that helps.
Sir
Is it possible for you to provide the code for ‘Single Trial – Phase Lock Statistic’?
Thanks
Sir,
would it be possible for you to post the code for ‘Single Trial – Phase Lock Statistic’ ?
Thanks
Sorry, I haven’t implemented phase locking statistic in MATLAB. Hope you can modify the PLV code so that it will suit your data.
Hello Praneeth,
Thanks so much for sharing this! I am new to PLV analysis (and EEG in general) and I don’t understand several things. I was hoping you could be able to clarify some of them. I am currently using BrainVision and I was hoping to run a similar PLV analysis in it. There is an add-on called Phase Locking Factor in BrainVision which I assume does a similar thing. It receives wavelets for the calculation of PLVs which have been transformed through Gabor filters (How is that different from Hilbert? Does it matter?).
Also, in typical ERP component analyses there are a lot of pre-processing steps (artifact rejection, filtering, (ICA?), baseline etc). When doing a PLV analysis do we do artifact rejection? Do we use a baseline like in regular ERPs?
Can we do a PLV using ERP components, that is, can I split an ERP component to its frequencies?
Some of my questions might be silly but as I said I am pretty new at this. 🙂
Any help will be greatly appreciated!
Thanks and thanks again for putting this together!
Litsa
Hi Litsa,
You’re actually asking good questions.
As far as I know, phase locking factor measures the consistency of the phase across trials in a channel, whereas PLV measures the consistency of the “difference in phase” between two channels across trials. They are mathematically very similar. Phase locking factor is a property of one channel, whereas PLV is a property of a pair of channels.
Yes, when I have used PLV analysis, I have rejected artifacts and band pass filtered my data before subjecting it to my PLV code.
In theory, yes, you can, but you should be asking yourself the purpose of your analysis. If you think different frequency components of an ERP have distinct underlying neural substrates, then it would make a lot more sense to split up your ERP component into its frequencies before analyzing phase locking. In the past, I have found PLV to be a very useful tool to give me an idea of dynamically changing functional connectivity patterns between signals from electrodes all over the brain.
Good luck!
Praneeth
Hi
I have a EEG data. Stimuli here is emotional video of 60s. I used 32 channel. If i use PLV it will give me 496 combination. How to observe this huge pattern. This is only for 1 band. If we consider 4/5 band how to say “This synchrony is significant”. Seeing the visualization we want to find out statement like. “For Higher Valance alpha band synchronization between P3 and C4 is significant”. Can you please help me to find out this question
Thanks
Rakib
Hi Rakib,
Thank you for your question. I wrote another script to solve this problem. https://praneethnamburi.wordpress.com/2011/08/18/connectedtopoplot/
I am personally a big fan of permutation tests to establish the significance of synchrony. I hope my post on the connected topoplot will help you.
Cheers,
Praneeth
Very good written post. It will be supportive to anybody who usess it, including myself. Keep up the good work – for sure i will check out more posts.
Thank you!
Hi there,
Thank you for this post! Hoping that you’re still following this thread… I have two questions. I’m analyzing EEG data and will be using PLV or phase coherence to look at phase synchronization between pairs of electrodes. I understand that PLV is different from coherence because it strictly takes instantaneous phase values and not amplitude values in the calculation, while coherence takes both amplitude and phase values. But how about phase coherence, which disregards the amplitude information? Can someone explain how PLV mathematically differs from phase coherence, and what that means in a layman’s language?? Second question: About how many repeated trials is enough to get a valid average PLV per person, if I’m interested in comparing groups? Say I have 90 participants, 30 in each of the 3 groups that I want to compare with each other, therefore I need to average PLV over trials per person, then within groups, and then compare the group averages. I would appreciate if anyone could help. Thanks so much!
Jung
Hi Jung, I follow this thread only rarely. Here is my opinion in case you still find it useful. As far as I can tell, phase synchronization is the same as PLV
http://www.scholarpedia.org/article/Measures_of_neuronal_signal_synchrony#Phase_synchronization
I’m not sure which expression you’re referring to when you say phase coherence.
Well, when I was analyzing my dataset, I got good PLV averages when I had about 500 trials. I don’t think you need quite as many per person, but more trials are definitely helpful!
Hi, and million thanks for your post. What would be the difference between computing the phase locked value and just the sliding window correlation between two time series? What is the extra info we get with the Hilbert transform? Another question: is the instantaneous amplitude given by the HT not exactly the same as the absolute value of the discrete signal? Thank you.
Another point, to calculate the INSTANTANEOUS PHASE I learned one must take the atan of the angle, inst_phase = atan(angle(hx)).
Dear Praneeth
Thank you for your code, it’s been very helpful. I have a question though. As a poor Fieldtrip user and a poorer Matlab user, could you be more specific in describing the cross-frequency phase-phase coupling. For example I would like to see if there is a phase locking between Theta and Alpha over occipital electrodes. In a previous answer, you said that it was better to duplicate your data and use two different filters, but I am not sure how to do that with your function.
Thanks again,
Quentin
Dear Praneeth,
I had sent you an email with my query. I am quoting it below. Looking forward to hearing from you on my question. Cheers!
“Hi Praneeth,
First of all, I would like to thank you for the brilliant code that you have written for calculating PLV. I took a look at your blog: https://praneethnamburi.wordpress.com/2011/08/10/plv/
I do ERPs at both cortical and subcortical levels to study auditory processing. I was wondering if it’s possible for getting a phase-locking value for say 1000 trials for just 1 channel from your code or a modification of your code. In other words, I would like to obtain a within-channel within-subject phase-locking value.
Thanks and bests, “
Hey Praneeth,
I have 15 minutes of data i have segmented in 15 segments of 1 minutes each = 1 minute x 15 segments.
I want to know what window interval length should i consider, can i calculate PLV over 60 seconds? should it be a moving window (10% overlapped) or should i choose randomly 5 seconds in the data and calculate PLV over it?
Regards,
Hasan Parvez
Biomedical Engineer
I have noticed you don’t monetize your blog, don’t waste your traffic, you can earn additional cash
every month because you’ve got high quality content. If you want
to know how to make extra $$$, search for: Mertiso’s tips best adsense alternative
Hello Praneeth,
Thank you for posting this script. I have a question: Is it possible to compute the single-trial PLV (i.e., Lachaux et al., 2000) by making some adjustments to the script? I would like to have a PLV measure for each trial individually instead of a mean across trials. I’m new to EEG connectivity analysis and I am not sure how to approach this.
Thanks in advance!
Thanks for your work! However, I think PLV is a function of omega, which is frequency. PLV is supposed to be done on the frequency domain. Your results return some value according to the time line, which makes me very confusing. Could you explain more?
I think the literature I read made a huge mistake, and makes me confusing…
Hello Praneeth,
Thank you for this valuable information about PLV. I just have a simple question regarding the trials-parameter, can we consider the acquired EEG data from n-subjects (having the same conditions) as an n-number of trials.
and in case we have only one trial, and as we know the phase lock value is the difference between instantaneous phases of two signals, then why do we need the input eegData as a multi-trial data?
Thank You
Thank you very much, very useful code and explanation
Hi! How would one calculate a phase-locking value between an EEG signal and an external stimulation signal (eg. audio, visual). Thank you!
Hi, I am trying to calculate PLV for each trial via using for loop but the size I am receiving id (1250x61x61) however this should be (1250x61x61X60) where 60 represents the number of trials can any one help me
Dear Praneeth,
Thank you for this post! I have two questions:
1. Is normalization before averaging across trials or before? When it comes to event related potential (ERP) calculation, baseline correction is always done before averaging across all the trials. (that is : channel * timepoints * trials (baseline corretion) -> channels * timepoints(averating across all the trials))
2. why not just remove the mean of the basline instead of doing the normalization?
Thank you for attention~~! Good day~!
Sansa
Excuse me, there are some mistakes about the first question…..
the first question is :
1. Is normalization done before averaging across trials or after it?
When it comes to event related potential (ERP) calculation, baseline correction is always done before averaging across all the trials. (that is : channel * timepoints * trials (baseline corretion) -> channels * timepoints(averating across all the trials))
I noticed that you did the averaging after you got the plv for each trial in your script.
I think it’s better to do it after basline correction just like doing ERP analysis, which is more reasonable
just from my point of view, of course : )
Hi Praneeth, thank you for making this script! We have a doubt, while testing various frequency bands we realized that the resulted figure from example.m script showed a high PLV value (almost to 1) at first and then drops to 0.1. This seems to be an artifact due to the fact that happens in every band and it lasts longer when changing the data points. E.g. in the case of theta (800 data points) it would last for almost 800msec (with a downsize sample of 1000Hz), while for gamma band (50 data points) it would last for 50msec.
Do you think could be an artifact? Are we missing something maybe? Sorry and thank you so much for any info you can give us!
Dear Praneeth
Thanks for your explanations.
I had two questions regarding PLV (and/or coherence):
1. Can I directly interpret the “grand average PLV values” or “grand average coherence values” as indicators of connectivity?
More explanation: These two measures seem to be some directionless correlation coefficients (like r-squared), right? If yes, so I guess I can directly interpret them? There is no P value attached to them. Still, I can say for example those above 0.7 are strong and those above 0.9 are excellent correlations. So can I look at the “Grand Average” PLVs (average of average PLVs of all subjects in a particular condition/group) and find those grand-average PLVs that are above, say, 70% across all the subjects, and list their responsible pairs of electrodes (channels) as strongly correlated and thus as “strongly functionally connected”? I can do the same for those between 50% and 70%, calling their electrodes (channels) to be moderately connected. Is this method possible? Please let me know about any other similar analyses I can do.
———————-
2. Can I treat these PLV or coherence values as some sort of “raw data” to be analyzed and compared statistically across subjects?
More explanation: Can I compare these PLV values or coherence values across all the different conditions (different interventions), using analyses such as ANOVA and post hoc tests? For example, let’s say we have 3 conditions, each with 30 subjects. And each subject has many, many PLV values between all possible pairs of electrodes. But the number of PLV values is the same for all subjects since all of them have been scanned with the same EEG device.
Can I compare each PLV value of all my 90 subjects (within 3 groups) with each other, in terms of their 3 conditions (interventions), using ANOVA and Tukey or some other appropriate statistical test?
I mean is it correct to treat these “correlation coefficients” named PLV or coherence as raw data, and statistically analyze them?
Thanks a lot in advance.
Vic
Great work! Thank you! I only have a small suggestion. use ‘filtfilt’ instead of ‘filter’ in your code so that transitional effects at the start and end of the signals are removed.
Hey Praneeth,
Thank you for sharing this knowledge. As PLV computes the consistency between two signlas, we should add two dataset to comput PLV. I checked the code and I saw the example. It is just with one dataset. Should we integrate both data of mother and infant and then run the code?
Thank you very much.